| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- 통신 프로토콜
- 리눅스
- Samba
- Git
- Type of Attacks
- mqtt
- protocol
- 오블완
- 명령어
- GitHub
- tftp
- Submodule
- Principles of Security
- tftpd-hpa
- 부팅 스크립트
- 스피커
- rfc 1350
- 네트워크
- 티스토리챌린지
- mosquitto
- 커밋 이력
- IOT
- 공유기 포트포워딩
- ubuntu 20.04
- virtualbox
- 가상머신
- 라즈베리파이5
- vm
- 라즈비안 os
- bfg repo-cleaner
신짱구의 개발일지
[컴퓨터보안] Public Key Infrastructure (Part 1) 본문
Symmetric Key Distribution
- 장점
- 대칭 키 분배 방식은 용량이 큰 메세지를 암호화하는데 있어서 비대칭 키 암호화 방식보다 더 효율적이라 빠르다.
- 한계점
- 대칭 키 분배 방식은 두 구성원 사이에 공유된 비밀 키가 필요하다.
- 그래서, n명의 사람이 있다면, n(n-1)/2 개의 비밀 키를 공유 한다.
- 문제점
- The number of keys
- 대칭 키 분배 방식: 각 통신 쌍마다 고유한 키가 필요
- 예시: 100명의 사용자가 서로 안전하게 통신하기 위해서 100*(100-1)/2 개의 고유 키가 필요하다.
- 비대칭 키 분배 방식: 각 사용자가 공개 키와 개인 키의 쌍을 가진다.
- 예시: 100명의 사용자가 있으면 각자에게 2개의 키(비밀키, 공개키)가 필요하므로 총 200개의 키만 필요하다. 각 사용자가 자신의 공개 키를 다른 사람과 공유하고, 비밀 키는 비밀리에 유지한다.
- 대칭 키 분배 방식: 각 통신 쌍마다 고유한 키가 필요
- The number of keys
- => 비대칭 키 분배 방식이 대칭 키 분배 방식에 비해 훨씬 더 적은 수의 키로 많은 사용자 간의 통신을 가능하게 한다.
- The distribution of keys is another problem
- 대칭 키는 통신하는 양쪽 모두에 의해 공유되어야 하고, 이 키가 안전하게 유지되어야 하는데, 키를 분배하는 과정에서 키가 노출되면 안전한 통신을 할 수 없다.
- 대칭 키를 안전하게 전달하기 위해서는 안전한 통신 채널이 필요한데, 그러한 채널을 설정하는 것이 도전적인 과제라 키가 제 3자에 의해 가로채지면 해당 키를 사용하는 모든 통신이 안전하지 않다.
- The distribution of keys is another problem
- Solution: 신뢰 가능한 third party 를 사용하자!
Key-Distribution Center(KDC): 1th solution
- KDC는 신뢰가능한 third party를 이용한 대칭 키의 문제에 대한 전형적인 해결책이다.
- 키의 수를 줄이기 위해, 각 호스트는 KDC 와의 공유된 비밀 키를 생성한다.
- 이렇게 각각의 모든 멤버들의 비밀 키는 KDC와 각 멤버 사이에 만들어진다.
- KDC의 문제점
- KDC의 데이터베이스는 공격자의 주요 타겟이 될 수 있다.
- KDC에서 문제가 발생하면, 전체 네트워크는 shutdown 된다.
- KDC에서 병목현상(communication bottleneck) 이 발생할 수 있다.
- 병목현상: 메모리가 작아서 한꺼번에 많은 양의 데이터가 유입되면 데이터를 처리한다고 컴퓨터가 느려지는 현상

Alice와 KDC 사이의 대칭키 VS Alice와 Bob 사이의 세션 키
- Alice와 KDC 사이의 symmetric key
- KDC는 각 멤버들과 통신에서 메세지를 보호하기 위해 위한 장기적인 비밀 키를 생성한다.
- Alice가 KDC에 접근할 때, 이 키를 사용하여 자신의 요청을 암호화하고, KDC는 같은 키를 사용해서 요청을 복호화한다.
- Alice와 Bob 사이의 session key
- KDC는 Alice와KDC 그리고, Bob과 KDC 2개의 고유한 대칭 키를 사용하여 Alice와 Bob사이에 세션 키를 생성한다.
- Alice와 Bob 사이의 특정 세션 또는 통신 기간 동안 한번만 사용되는 일시적인 키이다.
- Alice와 Bob 사이에 전송되는 모든 데이터를 암복호화 하는데 사용되고, 통신 세션이 종료되면 폐기된다.
Multiple Key-Distribution Center: 2th solution
- 단일 KDC 문제를 해결하기 위해 다수의 KDC를 사용하는 방법이다.
- We divide the world into domains.
- Each domain can have one or more KDCs.

Needham-Schroeder Protocol

1. Alice의 통신 요청: Alice는 자신 ID, Bob ID, 자신과 Bob을 식별하는 메세지를 서버에 보냄
2. KDC가 Kab를 생성하고, Alice가 Bob에게 전달할 수 있도록 Kb로 암호화된 복사본을 Alice에게다시 보낸다. Alice가여러 사람의 키를 요청할 수 있기 때문에 KDC 입장에서는 Alice가 보낸 고유한 nonce 메세지를 다시 보냄으로써 그 특정 메세지에 응답하고 있다고 확신시킨다. 또한, Bob의 이름을 포함하여 Alice에게 이 키를 공유할 사람이 누군지 알려준다.
3. Alice는 Bob에게 Kb로 해독할 수 있는 키를 전달해 데이터를 인증한다.
4. Bob은 Alice에게 키를 가지고 있다는 것을 보여주기 위해 Kab로 암호화된 nonce를 보낸다.
5. Alice는 Bob이 보낸 nonce에 간단한 연산을 수행하여 다시 암호화하여 보낸다. 다시 보내는 이유는 Alice가 키를 가지고 있고, 여전히 통신할 수 있는 상태라는 확신을 주기 위해서이다.
Otway-Rees Protocol

1. Alice가 Bob에게 Bob이 알 수 있는 정보와 Ra, R 복사본, Alice와 Bob의 identity를 Ka로 암호화한 Alice의 티켓을 전송한다.
2. Bob은 Alice에게 받은 티켓과 비슷한 본인의 ticket을 Kb로 생성해서 두 티켓을 KDC에게 보낸다.
3. KDC는 Bob에게서 받은 Ka와 Kb에 세션 키를 포함시켜 다시 Bob에게 보낸다.
4. Bob은 본인 티켓은 decryption하고, Alice에게 Alice의 티켓을 전송한다.
5. Alice는 Kab로 암호화된 짧은 메세지를 보내 session key를 가지고 있음을 증명한다.
Symmetric Key Agreement
- Alice와 Bob은 KDC 사용 없이 그들 사이에서 session key를 생성할 수 있다.
- session key 생성 방식을 Symmetric Key Agreement 라고 한다.
Diffie-Hellman Protocol

- Ex. Assume that g = 7 and p = 23
- Alice: x = 3 -> R1 = 7^3 mod 23 = 21
- Bob: y = 6 -> R2 = 7^6 mod 23 = 4
- Alice sends the number 21 to Bob.
- Bob sends the number 4 to Alice.
- Alice calculates the symmetric key K = 4^3 mod 23 = 18.
- Bob calculates the symmetric key K = 21^6 mod 23 = 18.
- The value of K is the same for both Alice and Bob
- g^xy mod p = 7^18 mod 23 = 18
- 𝐾 = (𝑔^𝑥 𝑚𝑜𝑑 𝑝)^𝑦 𝑚𝑜𝑑 𝑝 = (𝑔^𝑦 𝑚𝑜𝑑 𝑝)^𝑥 𝑚𝑜𝑑 𝑝 = 𝑔^𝑥𝑦 𝑚𝑜𝑑 𝑝
Analysis of Diffie-Hellman

- The secret key between Alice and Bob is made of three parts: g, x, and y
- 1/3 of the key is public: g
- The other 2/3 of the key: must be added by Alice and Bob
- Although the key in Alice’s hand (g, y, and x) and the key in Bob’s hand (g, x, and y), these two keys are the same because g^xy=g^yx.
- Although the two keys are the same, Alice cannot find the value of y used by Bob because the calculation is done in modulo p.
- 모듈로 p 연산은 일방향 함수(one-way function)라서 한 방향으로는 계산이 쉽지만, 역방향으로 계산하는 것은 매우 어렵다는 특징이 있다.
Diffie-Hellman Protocol 한계점
- 다음 두 공격에 취약
- Discrete logarithm attack -> R1과 R2로부터 x와 y를 찾아내서 key 계산 (매우 어렵)
- Main-in-the-Middle attack -> 통신 과정에서 중간자가 비밀스럽게 통신 내용을 가로채고 조작할 수 있는 보안 위협
- Eve는 Alice와 Bob 사이의 통신 채널에 침입한다.
- Alice와 Bob은 서로에게 공개 키를 보내지만, Eve는 Alice의 공개 키를 가로채서 자신의 공개 키로 대체해 Bob에게 전달한다.
- Bob의 공개 키도 Eve가 가로채서 Alice에게 Eve의 공개 키가 전달된다.
- 결과적으로, Alice는 Eve와의 비밀 키를, Bob은 또 다른 Eve와의 비밀 키를 각각 생성한다.
- Eve는 Alice와 Bob 사이의 모든 통신을 가로채고 복호화할 수 있을 뿐만 아니라, 내용을 변경하여 전달할 수 있다.

Station-to-station(STS) Protocol
- Diffie-Hellman 키 교환 방식 기반 Man-in-the-Middle Attack을 방지 프로토콜이다.
- Public key certificates 와 Digital signatures 를 사용해서 Alice와 Bob 사이에 session key를 설정하는 프로토콜이다.
- 작동방식
- 디지털 서명과 공개 키 인증서를 사용해서 각 당사자의 신원을 검증하여 Alice와 Bob이 서로의 공개 키가 실제로 상대방의 것인지 확신할 수 있게 한다.
- MITM 공격에서 공격자는 통신 과정에서 가로채서 자신의 메세지를 삽입하려고 시도하지만, STS 프로토콜에서는 Eve가 Bob의 개인 키를 위조할 수 없기 때문에, Alice에게 Bob인 척 할 수 없다.
- 예를 들어, 자신의 개인 키를 사용하여 메세지에 서명하면, 이 서명은 공개 키(인증)를 통해서만 검증될 수 있다.
- Eve는 Bob의 개인 키를 모르기 때문에 이 서명을 위조할 수 없다.

Public Key Distribution
- Public Announcement
- 공개 발표 방식은 Bob과 같은 사용자가 자신의 공개 키를 웹사이트에 게시하거나 신문에 광고하는 것과 같은 방법으로 공개한다.
- 문제점은 위조에 취약하다는 것이다. 만약 누군가 Bob의 웹 사이트를 해킹하거나 거짓 광고를 게재하여 잘못된 공개 키를 제공할 수 있다.
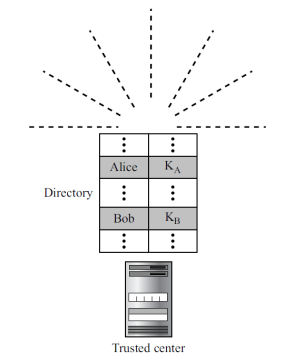
- Trusted Center
- 이 방식은 신뢰할 수 있는 중앙 기관이 공개 키 디렉토리를 가지고 있는 것이다.
- 이 디렉토리는 동적으로 업데이트되며, 각 사용자는 자신의 공개 키를 이 디렉토리에 제출하여 공개한다.
- 공개 발표 방식보다 안전하지만, 중앙 기관에 대한 신뢰가 필수적이다.
- Controlled Trusted Center
- 공개 키 발표에 타임스탬프가 포함되고, 인증 기관에 의해 서명될 수 있어서 응답의 가로채기와 변경을 방지한다.
- 그러나, 통신할 때마다 TC의 개입이 반드시 필요하다.

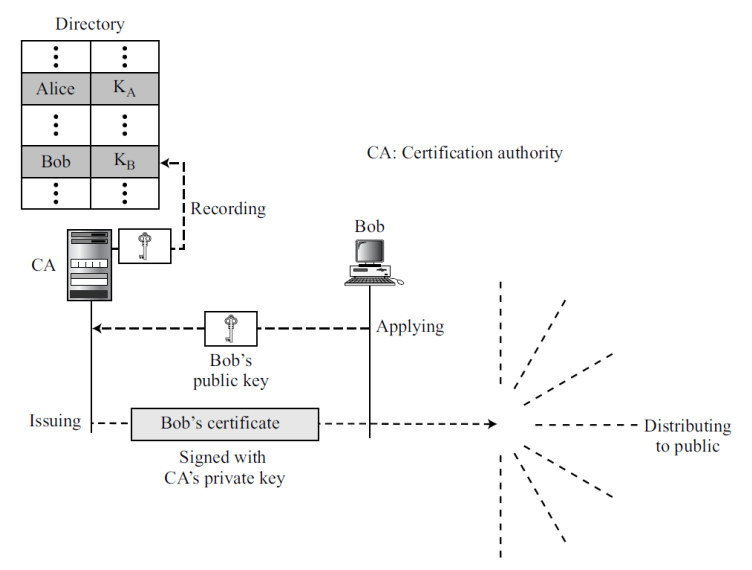
- Certification Authority (CA)
- CA는 단순히 certificate를 발급해주는 역할을 수행하고, 발급 후 통신에 참여할 필요는 없기 때문에 TC의 개입을 완화할 수 있다.
- Bob의 public key를 CA에 등록하면, 인증서 위조를 방지하기 위해 Bob의 public key에 CA의 개인 키로 서명하여 인증서를 발급한다.
- CA 자체의 공개 키는 잘 알려져 있으며 위조될 수 없다.